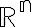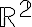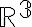- Profesor: Edgar Roman Arce Santana
Cursos disponibles
- Profesor: Edgar Roman Arce Santana
Procesamiento Digital de Señales
Semestre Enero - Agosto 2020
Este curso tiene como objetivos:
- Que el alumno comprenda los conceptos básicos de señales y sistemas en tiempo discreto, así como su representación en el dominio de la frecuencia y en el dominio z.
- Que el alumno sea capaz de implementar sistemas digitales FIR e IIR en un lenguaje de alto nivel como MATLAB o C/C++, y de diseñar filtros digitales simples para aplicaciones específicas.
Temario:
- Señales y sistemas en tiempo discreto
- La transformada z
- Representación en el dominio de la frecuencia
- Transformada discreta de Fourier
- Muestreo y reconstrucción de señales
- Diseño de filtros digitales
Horarios de clases presenciales:
- Martes 8:00 – 10:00 horas Centro de Cómputo – Edificio 1
- Jueves 8:00 – 10:00 horas Salón 304
- Viernes 9:00 – 10:00 horas Salón 304
Asesorías académicas:
- Cubículo C-418 (Edificio 1, Facultad de Ciencias)
- Miércoles, 13:00 – 14:00 horas
- Política de puertas abiertas
Bibliografía recomendada:
- Tratamiento de señales en tiempo discreto. Oppenheim y Schafer, 2ª. Edición, Ed. Prentice Hall, 2000.
- Tratamiento digital de señales: Principios, algoritmos y aplicaciones, Proakis y Manolakis. 3ª. Edición, Ed. Prentice Hall, 1998.
- Signals and Systems. Haykin y Van Veen, John Wiley & Sons Inc., 2005.
- Profesor: Bersaín Alexander Reyes
Semestre Enero - Agosto 2020
Este curso tiene como objetivos:
- Que los alumnos sean capaces de derivar, entender, implementar y aplicar algunos de los métodos numéricos más comunes, e.g. soluciones de sistemas de ecuaciones lineales y regresión lineal
- Que los alumnos incrementen sus habilidades y experiencia en programación y conozcan el uso de entornos especializados para el cómputo numérico, como MATLAB
- Introducción a MATLAB
- Solución de ecuaciones no lineales
- Sistemas de ecuaciones lineales
- Interpolación
- Regresión lineal por mínimos cuadrados
- Integración y diferenciación numérica
Horarios de clases presenciales:
- Martes 10:00 – 12:00 horas Salón 101
- Jueves 10:00 – 12:00 horas Centro de Cómputo – Edificio 1
- Viernes 11:00 – 12:00 horas Salón 101
Asesorías académicas:
- Cubículo C-418 (Edificio 1, Facultad de Ciencias)
- Lunes, 14:00 – 15:00 horas
- Política de puertas abiertas
Bibliografía recomendada:
- S.C. Chapra, R.P. Canale. Métodos Numéricos para Ingenieros. Ed. Mc Graw-Hill, 5a. Edición, 2007
- R.L. Burden, J.D. Faires. Análisis Numérico. Thompson Editores, 2001
- S.M. Dunn, A. Constantinides, P.V. Moghe. Numerical Methods in Biomedical Engineering. Academic Press, 2005
- J.H. Mathews, K.D. Fink. Numerical Methods using MATLAB, Prentice Hall, 3a. Edición, 2005
- Profesor: Bersaín Alexander Reyes
- Profesor: Valdemar Arce
Programación Básica 2020
En este curso se establecen las bases para la programación estructurada, enfocándose en los siguientes conceptos:
1.- Importancia de la programación en la ingeniería
2.- Entrada y salida básica en consola
3.- Operadores aritméticos y funciones matemáticas
4.- Manejo de variables y tipos de datos básicos
5.- Estructuras de decisión
6.- Estructuras de iteración
7.- Funciones
8.- Arreglos
Para el curso se utilizarán lenguajes "tipo C"; es decir, lenguajes que comparten la estructura y sintaxis general del lenguaje C. Este tipo de lenguajes es muy amplio (C, C++, Java, Processing, C#, Objective-C, etc) y de amplio uso en la academia y la industria. Principalmente utilizaremos Processing, y C++ como lenguaje secundario.
Horarios:
Martes de 12:00 a 14:00 en el Centro de Cómputo del Edificio 1
Jueves de 12:00 a 14:00 en el Salón 302
Viernes de 13:00 a 14:00 en el Salón 302
Horarios de atención a alumnos:
Lunes y Miércoles de 12:00 a 14:00 en la oficina TA-209 (segundo piso de la Torre, a un lado de la consejería).
- Profesor: Francisco Alfonso Alba Cadena
Programación Numérica 2020
En este curso se consolidarán los conocimientos de múltiples materias como Cálculo Diferencial, Cálculo Integral, Álgebra Superior, Álgebra Matricial, Programación Básica y Programación Avanzada para estudiar e implementar algoritmos que permitan realizar cálculos complejos. El programa del curso se resume como sigue:
1.- Introducción a Python y NumPy
2.- Solución de ecuaciones no lineales
3.- Solución de sistemas de ecuaciones lineales
4.- Interpolación
5.- Regresión lineal
6.- Diferenciación e integración numéricas
Para el curso se utilizará el lenguaje Python, el cual actualmente es uno de los más utilizados en la academia y en la industria. En particular se recomienda instalar la distribución Anaconda (versión 3.7), la cual incluye las librerías requeridas (NumPy y MatPlotLib) así como entornos de programación sofisticados (Spyder y Jupyter Notebook).
Horarios:
Martes de 10:00 a 12:00 en el Centro de Cómputo del Edificio 1
Jueves de 10:00 a 12:00 en el Salón 302
Viernes de 11:00 a 12:00 en el Salón 302
Horarios de atención a alumnos:
Lunes y Miércoles de 12:00 a 14:00 en la oficina TA-209 (segundo piso de la Torre, a un lado de la consejería).
- Profesor: Francisco Alfonso Alba Cadena
- Profesor: Miguel Velazquez
- Profesor: Miguel Velazquez
- Profesor: Miguel Velazquez
PROCESAMIENTO DIGITAL DE SEÑALES (PRIMAVERA 2018)
Horario Oficial: Martes y Jueves 8:00 - 10:00 hrs, Viernes 8:00-9:00 hrs, Salón # 303, Campus Pedregal, Facultad de Ciencias.
Instructor: Dr. Daniel U. Campos Delgado, Cubículo 414, Edificio 1, Campus Pedregal, Email: ducamposdelgado@hotmail.com, Página WEB: http://galia.fc.uaslp.mx/~ducd/
Libro de Texto: ``Tratamiento Digital de Señales'', J.G. Proakis y D.G. Manolakis, 4a. Edición, Prentice Hall, 1996.
Libros de Referencia:
``Discrete-Time Signal Processing'', A.V. Oppenheim y R.W. Schafer, Prentice Hall, 1989.
``Procesamiento de Señales Analógicas y Digitales'', A. Ambardar, Ed. Thomson Learning, 2002.
``System and Signal Analysis'', C.T. Chen, Oxford University Press, 1994.
Descripción del Curso
Introducción (Capitulo I, 1.1-1.4)
Señales y Sistemas en Tiempo Discreto (Capitulo II, 2.1-2.5.1)
Transformada Z (Capitulo III, 3.1-3.3 \& 3.5-3.6)
Análisis en Frecuencia (Capitulo IV, 4.1-4.5)
Transformada Discreta de Fourier (Capítulo V, 5.1-5.3)
Implementación de Sistemas Discretos (Capítulo VII, 7.1-7.3)
Diseño de Filtros Digitales (Capítulo VIII, 8.1-8.5)

- Profesor: Daniel Ulises Campos Delgado
Los objetivos del curso son:
Los principales temas que se ven en este curso son:- Profesor: Jesús Gilberto Rodríguez Escobedo
Los objetivos del curso son:
- Que el estudiante adquiera habilidad para resolver ecuaciones diferenciales.
- Proporcionar y desarrollar las herramientas que permitan aplicar las ecuaciones diferenciales en el modelado de sistemas para que el estudiante comprenda la capacidad de predicción de resultados reales de un modelo.
- Introducción a las ecuaciones diferenciales y sus soluciones.
- Ecuaciones diferenciales ordinarias de primer orden y sus aplicaciones.
- Ecuaciones diferenciales ordinarias de orden superior y sus aplicaciones.
- Soluciones en serie de potencias.
- Transformada de Laplace e introducción a los sistemas lineales.
- Profesor: Jesús Gilberto Rodríguez Escobedo
El curso de Fisiología comprende el estudio de las funciones de las células, órganos y sistemas del cuerpo humano. Especial énfasis en las funciones del cuerpo humano desde el punto de vista de la ingeniería biomédica.
- Profesor: Ricardo Espinoza Tanguma
- Profesor: Anna Lena Di Carlo
OBJETIVOS GENERALES
El objetivo es hacer que el estudiante será capaz de diseñar, implementar, y depurar algoritmos sencillos en lenguaje C/C++. El estudiante adquirirá los conocimientos básicos de las estructuras de decisión, ciclos de repetición, funciones y arreglos unidimensionales.

- Profesor: Ruth Mariela Aguilar Ponce
- Profesor: Kenya Crisóstomo
- Profesor: JONATHAN ENRIQUE MARTINEZ MEDINA
- Profesor: Kenya Crisóstomo
- Profesor: Sergio Dávila Espinosa
- Profesor: Kenya Crisóstomo
- Profesor: Sergio Dávila Espinosa
- Profesor: Daniel Ulises Campos Delgado
- Profesor: Martín Luna Rivera
Digital Image processing is part of the Master in Electronics Engineering. The main objective of the course is to understand and applied image enhancement algorithms in the spatial and frequency domain.

- Profesor: Ruth Mariela Aguilar Ponce
Curso de Evaluación de Fuandamentos de Programación
Maestría en Ingeniería Electrónica
- Profesor: Ruth Mariela Aguilar Ponce
This course is an introduction to Programming Projects in C/C++. The main objective is that the student acquire experience implementing signal processing algorithms in C++.

- Profesor: Ruth Mariela Aguilar Ponce
Estudiar y aplicar los conceptos básicos de programación
estructurada en un lenguaje de alto nivel. Al final del curso,
el alumno deberá ser capaz de diseñar, implementar, y
depurar algoritmos sencillos en lenguaje C/C++.

- Profesor: José de Jesús Ramírez García
Entender y aplicar los conceptos básicos sobre
programación orientada a objetos, tales como: definición de
clases, objetos y métodos, sobrecarga de funciones y
operadores, herencia y polimorfismo. Conocer las clases y
funciones para manejo de archivos en C++.

- Profesor: José de Jesús Ramírez García
El curso cubre los aspectos teóricos y prácticos en la planeación y montaje de una infraestructura apropiada para el desarrollo de aplicaciones en Internet. El curso contiene dos ingredientes básicos: infraestructura y aplicaciones. Al final el estudiante será capaz de evaluar, construir y programar un sistema de información para su uso inmediato en Internet.

- Profesor: José de Jesús Ramírez García
- Profesor: Armando Arce Casas
Objetivo:
El curso de tecnologías de Internet introduce al estudiante al estado actual en el área. La organización del contenido temático le permitirá revisar el potencial de aplicabilidad del Internet en un curso introductorio, pero actualizado con las principales tecnologías disponibles del lado del cliente utilizadas hoy día en los principales visores de páginas web.

- Profesor: José de Jesús Ramírez García
Esencialmente, este curso tiene como propósito el estudio de las técnicas y procesos de los sistemas de comunicación digital, como son las comunicaciones por pulsos codificados así como los métodos de muestreo, codificación y detección.
- Profesor: Marco Aurelio Cárdenas Juárez
- Profesor: Martín Luna Rivera
- Profesor: José Salomé Murguía
Objetivos del Curso son:
- Que el estudiante sea capaz de utilizar los conceptos básicos del Cálculo Integral en el planteamiento y solución de problemas de matemáticas, física e ingeniería.
- Que el alumno extienda los conceptos de Cálculo Diferencial y conjuntarlos con los de Cálculo Integral en la resolución de problemas.
- Integración
- Funciones logarítmicas, exponenciales, trigonométricas, trigonométricas, inversas e hiperbólicas.
- Aplicaciones de la integración.
- Técnicas de Integración.
- Profesor: Jesús Gilberto Rodríguez Escobedo
- Profesor: Miguel Velazquez
- Profesor: Stephanie Velazquez
- Profesor: Jose Luis T. X.
Objetivo de la Asignatura:
- QUE EL ALUMNO OBTENGA LOS CONOCIMIENTOS Y HABILIDADES FUNDAMENTALES PARA EL ANÁLISIS Y DISEÑO DE SISTEMAS ELECTRÓNICOS DIGITALES.
- QUE EL ESTUDIANTE CONOZCA Y DOMINE EL USO DE TÉCNICAS DE ANÁLISIS Y SIMPLIFICACIÓN DE CIRCUITOS LÓGICOS.
- QUE EL ALUMNO APRENDA EL USO DE HERRAMIENTAS DE CAD PARA EL ANÁLISIS Y DISEÑO DE CIRCUITOS DIGITALES

- Profesor: Ruth Mariela Aguilar Ponce
Comprender las características de los sistemas móviles como plataforma de diseño y los retos para la programación de aplicaciones. Aplicar los conocimientos básicos para la implementación de aplicaciones que involucre el procesamiento de señales. Comprender el proceso de optimización de las aplicaciones para un buen funcionamiento en los dispositivos móviles
- Profesor: Ruth Mariela Aguilar Ponce
- Profesor: José Salomé Murguía
Este es un curso usual sobre diferenciación de funciones de varias variables. Los temas tratados son:
- Conjuntos, funciones y el espacio euclidiano Rn
- Nociones de topología de Rn
- Sucesiones en Rn
- Continuidad de funciones de varias variables
- Diferenciabilidad de funciones de varias variables
- Profesor: Antonio Morante Lezama
Este es un curso usual sobre integración de funciones de varias variables y cálculo vectorial. Los temas tratados corresponden aproximadamente a la parte III (Integrales dobles e integrales sobre curvas) y a la parte IV (Integrales triples e integrales sobre superficies) del libro:
Calculus of Several Varibles (Third Edition) de Serge Lang. Springer. 1987
Temario:
- Integrales dobles
- Integrales sobre curvas
- El Teorema de Green
- Integrales triples
- Integrales sobre superficies
- Profesor: Antonio Morante Lezama
Ejercicios y archivos de GeoGebra, wxMaxima y Octave de apoyo para el curso de SIstemas DInámicos. Los temas que se tratan son:
- Conceptos básicos
- Dinámica simbólica
- Caos y estabilidad estructural
- Aplicación: el método de Newton
- Profesor: Antonio Morante Lezama
Este es un curso sobre gestión de la calidad , que incluyede técnicas usuales para el control estadístico de procesos usando R. Los temas que se tratan son:
- Gestión de la calidad y control de procesos
- Herramientas estadísticas básicas para el control de procesos
- Gráficos de control de Shewhart para variables
- Gráficos de control de Shewhart para atributos
- Gráficos de control para vectores de variables
- Profesor: Antonio Morante Lezama
Este es un curso introductorio de aplicaciones de métodos numéricos en la geometría del diseño asistido por computadora. La implementación de los algoritmos presentados se ha hecho con el sistema de álgebra computacional Maxima. Los temas que se tratan son:
- Interpolación (optativo como repaso)
- Polinomios de Bernstein y curvas de Bézier - De Casteljau
- Interpolación segmentada
- Aplicación a las ecuaciones diferenciales ordinarias
- B-splines
- Superficies de Bézier - De Casteljau
- Profesor: Antonio Morante Lezama
Este es un curso estándar de algebra de matrices. Los temas que se tratan son:
- Matrices y vectores
- Sistemas de ecuaciones lineales
- Matrices no singulares
- Determinantes
- Valores y vectores propios
- Profesor: Antonio Morante Lezama
Este es el complemento de un curso estándar de métodos numéricos, los cuales se implementan aquí usando Octave. Los temas que se tratan son:
- Errores, condicionamiento, estabilidad y costo
- Sistemas de ecuaciones lineales: métodos iterativos
- Sistemas de ecuaciones no lineales
- Valores y vectores propios
- Problemas de valor inicial
- Problemas de valores a la frontera
- Ecuaciones diferenciales parciales
- Introducción al método de los elementos finitos
- Profesor: Antonio Morante Lezama
Este es un curso estándar de métodos estadísticos multivariados, los cuales se implementan usando R. Los temas que se tratan son:
- Conceptos básicos de estadística multivariada
- Tratamiento preliminar de datos multivariados
- Análisis exploratorio de datos multivariados
- Análisis de cúmulos
- Análisis de componentes principales
- Análisis multivariado de la variancia
- Análisis de regresión lineal múltiple
- Análisis discriminante y regresión logística(optativo)
- Análisis de correlación canónica (optativo)
- Escalamiento multidimensional (optativo)
- Profesor: Antonio Morante Lezama
Este es un curso estándar de métodos numéricos, los cuales se implementan usando Octave. Los temas que se tratan son:
- Introducción a Octave
- Tipos de error
- Ecuaciones no lineales
- Sistemas de ecuaciones lineales
- Interpolación
- Ajuste de curvas
- Diferenciación numérica
- Integración numérica
- Profesor: Antonio Morante Lezama
Este es un curso estándar de métodos estadísticos univariados, los cuales se implementan usando R. Los temas que se tratan son:
- Conceptos básicos de Estadística
- Guía corta de R
- Análisis exploratorio de datos univariados
- Análisis exploratorio de datos bivariados
- Probabilidad: simulada con R
- Estimación de parámetros
- Pruebas de hipótesis
- Análisis de regresión lineal simple
- Análisis de la variancia
- Profesor: Antonio Morante Lezama
- Profesor: Miguel Velazquez
- Profesor: Miguel Velazquez
- Profesor: Stephanie Velazquez
Quimica, el estudio del cambio
- Profesor: Martha Yolanda Barron Manzanares
Examinar el uso de las ecuaciones diferenciales para representar un sistema dinámico y analizar sus métodos básicos de solución.
Deducir los modelos matemáticos que describen el crecimiento de poblaciones y de interacción entre especies, y analizar el
comportamiento de sus soluciones en función de los parámetros del modelo.
- Profesor: Byanka Espinoza

Al finalizar el curso el estudiante será capaz de conocer los conceptos fundamentales de la ecotoxicología y aplicarlos para comprender la relación entre los efectos en biota ocasionados por diferentes agentes estresantes originados por el ser humano y, el cómo puede ser usada para el diseño de estrategias de intervención para la protección de la diversidad biológica.
- Profesor: Cesar ilizaliturri

- Profesor: Martha Yolanda Barron Manzanares
El curso de Introducción a la Biología Molecular tiene como objetivo:
Analizary comprender la estructura, composición y función de los ácidos nucleicos. Entender las diferencias entre el DNA y el RNA, así como las funciones para los distintos tipos de RNA. Entender los principios básicos de algunos procesos moleculares esenciales para la vida, incluyendo la duplicación del DNA, la transmisión de la información del DNA a moléculas de RNA, y finalmente la síntesis de proteínas a partir de RNA mensajero. Comprender los distintos mecanismos moleculares por los que el DNA dañado es reparado en las células de los organismos eucariontes. Conocer y entender los principios de las técnicas de DNA recombinante. Los objetivos de este curso contribuyen al desarrollo de competencias profesionales en las que el alumno será capaz de identificar, analizar y proponer soluciones para resolver problemas científicos y prácticos en el área de biología molecular.
- Profesor: MARGARITA RODRIGUEZ Y DOMINGUEZ KESSLER
OBJETIVO. Presentar al estudiante los conceptos demográficos básicos y de historia de vida empleados en el estudio de la ecología y dinámica de poblaciones silvestres. El alumno será capaz de reconocer los factores bióticos y abióticos que determinan las estrategias de comportamiento de los organismos, las cuales a su vez modelan los parámetros de historia de vida. El estudiante aprenderá técnicas de estimación, clásicas y novedosas, para obtención de parámetros poblacionales, aprenderá a generar tablas de vida y a estimar parámetros demográficos a partir de la aplicación de herramientas estadísticas actuales. Al término del curso el estudiante será capaz de desarrollar e interpretar modelos estadísticos empleados para la estimación de parámetros biológicos y poblacionales.
- Profesor: Vanessa Labrada Martagón
OBJETIVO: Al finalizar el curso el alumno conocerá los conceptos básicos de estadística multivariada para su aplicación al análisis de información biológica. Los objetivos de este curso contribuyen al desarrollo de competencias profesionales en las que el alumno será capaz de identificar y analizar problemas, así como plantear, resolver y explicar soluciones a problemas científicos y prácticos en áreas de especialización de estadística aplicada multivariada.
- Profesor: Vanessa Labrada Martagón
Conocer los conceptos generales de lo que es el desarrollo sustentable en el contexto económico, social y ambiental de nuestro país, así como generar conciencia en el alumno del impacto que ha tenido el ser humano en nuestro planeta.
RECURSOS BIBLIOGRÁFICOS
- Gerd Michelsen y Marco Rieckman. 2008. Programa de Maestría Internacional “Sustainable Development and Management”. Vol. 2: Introducción al Desarrollo Sustentable.
- INEGI. 2000. Indicadores de desarrollo sustentable en México, Instituto Nacional de Estadística, Geografía e Informática.
- José Adrián Figueroa Hernández. 2001. Los nuevos protagonistas del desarrollo sustentable en los albores del siglo XXI. Secretaría de Ecología y Gestión Ambiental.
- LEGEPA. 2003. Ley general del equilibrio ecológico y la protección al ambiente (y disposiciones complementarias), Edición: 21a actualizada, Porrúa.
- Leopoldo García, Colín Scherer y Mariano Bauer Ephrussi. 1996. Energía, ambiente y desarrollo sustentable: (El caso de México), UNAM.
- Miller, G. Tyler. 1994. Ecología y medio ambiente : introducción a la ciencia ambiental, el desarrollo sustentable y la conciencia de conservación del planeta tierra. Ed. Iberoamérica.
- Reynol Díaz Coutiño. 2015. Desarrollo Sustentable, una oportunidad para la vida, Tercera edición. Ed. Mc Graw Hill Education.
APOYO ELECTRÓNICO
- FAO
http://www.fao.org/publications/en/
- SEMARNAT
- CONABIO
- NORMAS OFICIALES MEXICANAS
http://www.cmic.org/comisiones/Sectoriales/medioambiente/Varios/Leyes_y_Normas_SEMARNAT/NOM/nom.htm
- IUCN Red List
- CITES
https://cites.org/eng/disc/species.php
- Catálogo Nacional de Indicadores
http://www3.inegi.org.mx/sistemas/cni/
- Calcula tu huella ecológica, WWF
http://www.tuhuellaecologica.org/
- Programa de las Naciones Unidas para el Medio Ambiente
- Programas de Manejo ANPs
https://www.gob.mx/conanp/acciones-y-programas/programas-de-manejo?idiom=es
- Proyecto de Evaluación de las UMAS Página de Conabio
http://www.biodiversidad.gob.mx/usos/UMAs.html
UNESCO
SEMARNAT Consultas Públicas de Proyectos de Impacto Ambiental Vigentes
http://www.semarnat.gob.mx/impacto-ambiental/consultas-publicas/consultas-vigentes

- Profesor: Vanessa Labrada Martagón
Este es un curso básico sobre el uso de software que puede ser de utilidad en el ámbito de las ciencias y la tecnología, en particular en Matemáticas. Los temas que se tratan son:
- Algo sobre informática
- El sistema operativo GNU/Linux
- Preparación de documentos con LaTeX
- Cálculos numéricos con GNU Octave
- Cálculos estadísticos con R
- Cálculos simbólicos con Maxima
- Matemáticas dinámicas con GeoGebra
- Profesor: Antonio Morante Lezama
- Profesor: Adán Rodriguez
- Profesor: Adán Rodriguez
El seminario de comunicación científica es un curso obligatorio en el primer semestre de la maestría y doctorado en el que el alumno ejercitará sus habilidades de redacción y comunicación de ideas, conceptos y avances científicos. El objetivo es que el estudiante adquiera experiencia que hará más fácil la publicación de los resultados de su labor científica en el futuro. Algunas de las tareas se pedirán en inglés para fortalecer las habilidades de comunicación en esta lengua.

- Profesor: Pedro Ruiz Diaz
CalcPlot3D es una aplicación interactiva en línea (applet), creada por Paul Seeburger, para visualizar objetos utilizados en cursos de cálculo de varias variables, física, ecuaciones diferenciales, etc.
Temario del taller.
- Qué es CalcPlot3D, para qué y cómo usarlo.
- Áreas, íconos, páneles y objetos básicos de CalcPlot3D.
- Ejemplos:
- Curvas paramétricas en el plano.
- Curvas paramétricas en el espacio.
- Diferenciación de funciones de varias variables.
- Integración múltiple.
- Cálculo vectorial.
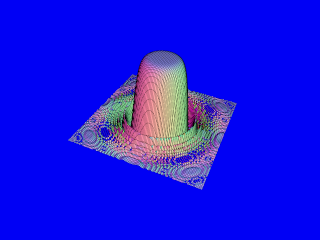
- Profesor: Antonio Morante Lezama
Omitir categorías